pulling the rabbit out of the hat??

At the end of the previous blog, I mentioned that the topological properties of the Cantor space make it searchable via a constructive algorithm. Surprisingly, its not too much of a lift but still feels kinda magical. Not only are we deciding a total predicate without any a priori information other than continuity and compactness. Nothing else is known ahead of time: which bit indices will be queried, the number of bits that are required, or any details about the frontier itself. All of this information is extracted at execution time.

In a world of AI generated images, enjoy my hand-drawn rendition of a rabbit in a hat¹. I know it is shit. Sorry.

haskell wizardry

sme :: Pred -> IO [Prefix]
sme p = go IM.empty where
  go asg = case evalP p asg of
    Right True -> pure [asg]
    Right False -> pure []
    Left i -> do
      f0 <- go (IM.insert i False asg)
      f1 <- go (IM.insert i True asg)
      pure (f0 ++ f1)

This performs a determinsitic DFS of the decision tree induced by the predicate p: (\mathbb{B}^\mathbb{N} \rightarrow \mathbb{B}) \rightarrow \mathbb{B} via a partial oracle that answers onl ythe bits present int eh current prefix \sigma and raises a Need exception when p demands an unknown bit index i (this is all covered in the previous blog, nothing new here).

In this case, at node \sigma we now have three cases: 1. evalP returns True = p is already a constant 1 on [\sigma] cylinder set so we can record \sigma and return 2. evalP returns False, so [\sigma] \subseteq U^c so the entire branch can be pruned 3. It raises Need i so we branch to \sigma \cup \{i \mapsto 0 \} and \sigma \cup \{i \mapsto 1 \}.

The result of this procedure is \cal{F} = \text{SME}(p), which represents the set of minimal true prefixes (an antichain² fo finite \sigma with p \equiv 1 on [\sigma]). Topologically, the preimage U = p^{-1}(1) (which represents the set of satsifying assignments) can be expressed as the following disjoint union of cylinders

U = \bigcup_{\sigma \in \cal{F}} [\sigma]

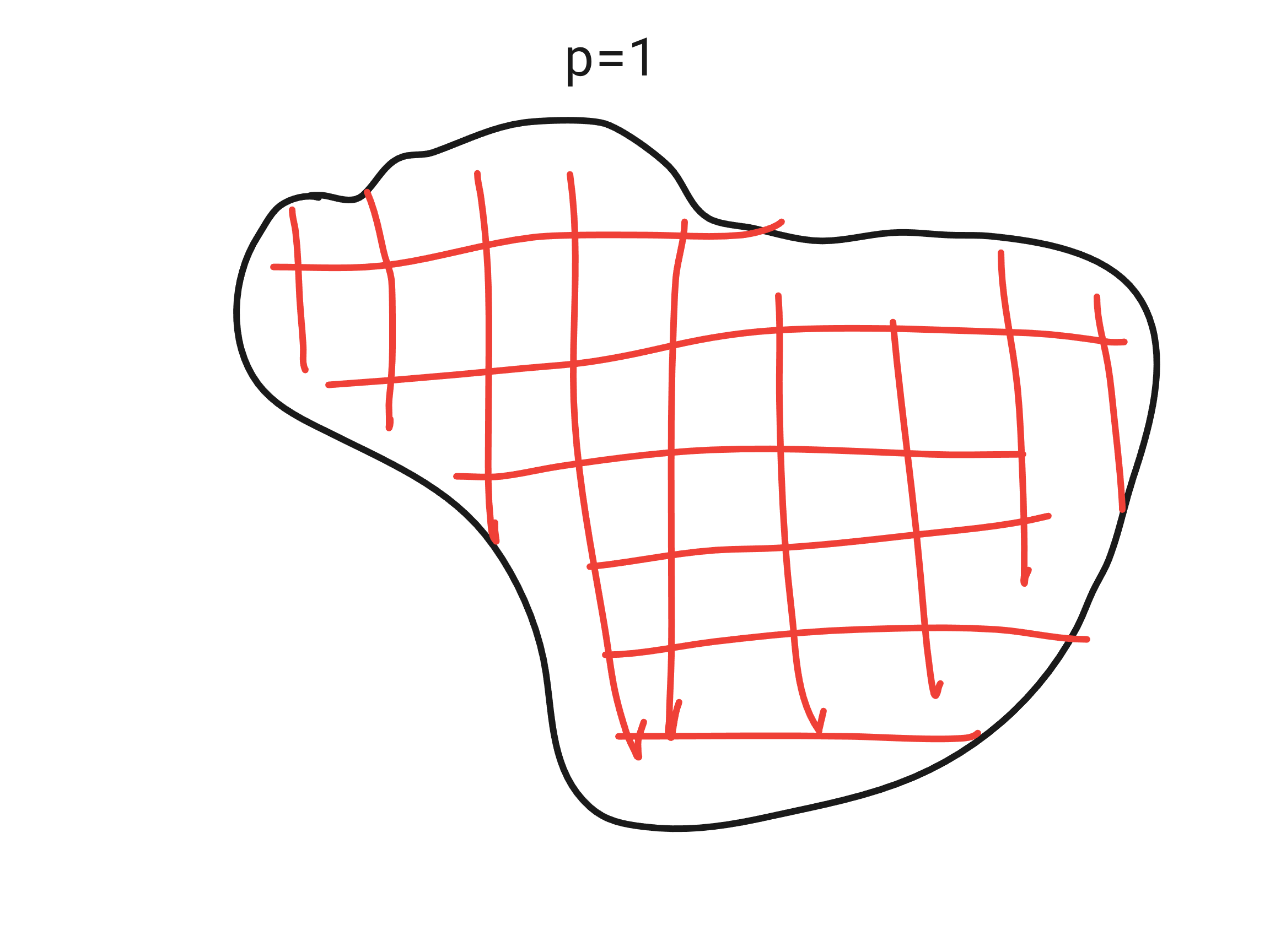Imagine each prefix \sigma as carving out a subcube (cylinder set) of all points that agree with \sigma. Then taking the union fills up the region where U = p^{-1} (1). By compactness, there is always a finite subcover but our algorithm refines this so that they are also disjoint.

examples

-- fib-eventually (7 cylinders)

\x -> any (\f -> f < 30 && x f) (takeWhile (< 30) fibonacci)

This checks: “Does the infinite binary sequence x have True at any Fibonacci position < 30?”

The 7 cylinders represent the minimal decision tree: - If x[1] = True = predicate is True (fib 1) - Else if x[2] = True = predicate is True (fib 2) - Else if x[3] = True = predicate is True (fib 3) … and so on for positions 5, 8, 13, 21

-- prime-eventually (8 cylinders)

\x -> any (\p -> p < 20 && x p) (takeWhile (< 20) primes)

This computes primes on-demand from primes = filter isPrime [2..] (infinite list), then checks if x is True at any prime position < 20. The 8 cylinders correspond to checking positions 2, 3, 5, 7, 11, 13, 17, 19 in sequence.

-- collatz-reaches-1 (942 cylinders!)

\x -> let collatz n = if even n then n `div` 2 else 3*n+1
        orbit n = takeWhile (/= 1) (iterate collatz n)
    in length (orbit (sum [i | i <- [0..9], x i] + 1)) < 50

Again expanding this gives us: 1. Takes first 10 bits of x, sums the indices where x[i] = True, adds 1 2. Computes the Collatz orbit of that number (3n+1 conjecture) 3. Checks if the orbit reaches 1 in < 50 steps

Certain predicates over infinite sequences can be decided by examining only finite prefixes, and algorithms like sme can discover these finite characterizations. I wonder if there is something interesting in representing this as finite automata. In the next blog, we’ll go into some implications of introducing Randomness.