Private Money: Part 3
Background
Double-spending is when someone tries to use the same funds more than once. It’s a fundamental problem in finance that appears in various guises. In traditional banking, this looks like check kiting—manipulating the float time between accounts to cover overdrafts. A notorious example is Najeeb Khan’s $180M fraud, where he exploited bank timing windows to fund a lavish lifestyle at the expense of clients.
In crypto, Ethereum Classic suffered multiple 51% attacks in 2020 where attackers rewrote transaction history and double-spent over $9M. This showed that public blockchains without secure consensus can be vulnerable too.
Zcash presents a more complex challenge: its shielded transactions reveal nothing about sender, receiver, or value. To prevent double-spending while preserving privacy, Zcash enforces two cryptographic constraints:
- Private inclusion proof: The note1 must be in the note-commitment Merkle tree.
- Public non-inclusion proof: The note’s nullifier must not be in the nullifier set.
Why Zcash uses a public non-inclusion check
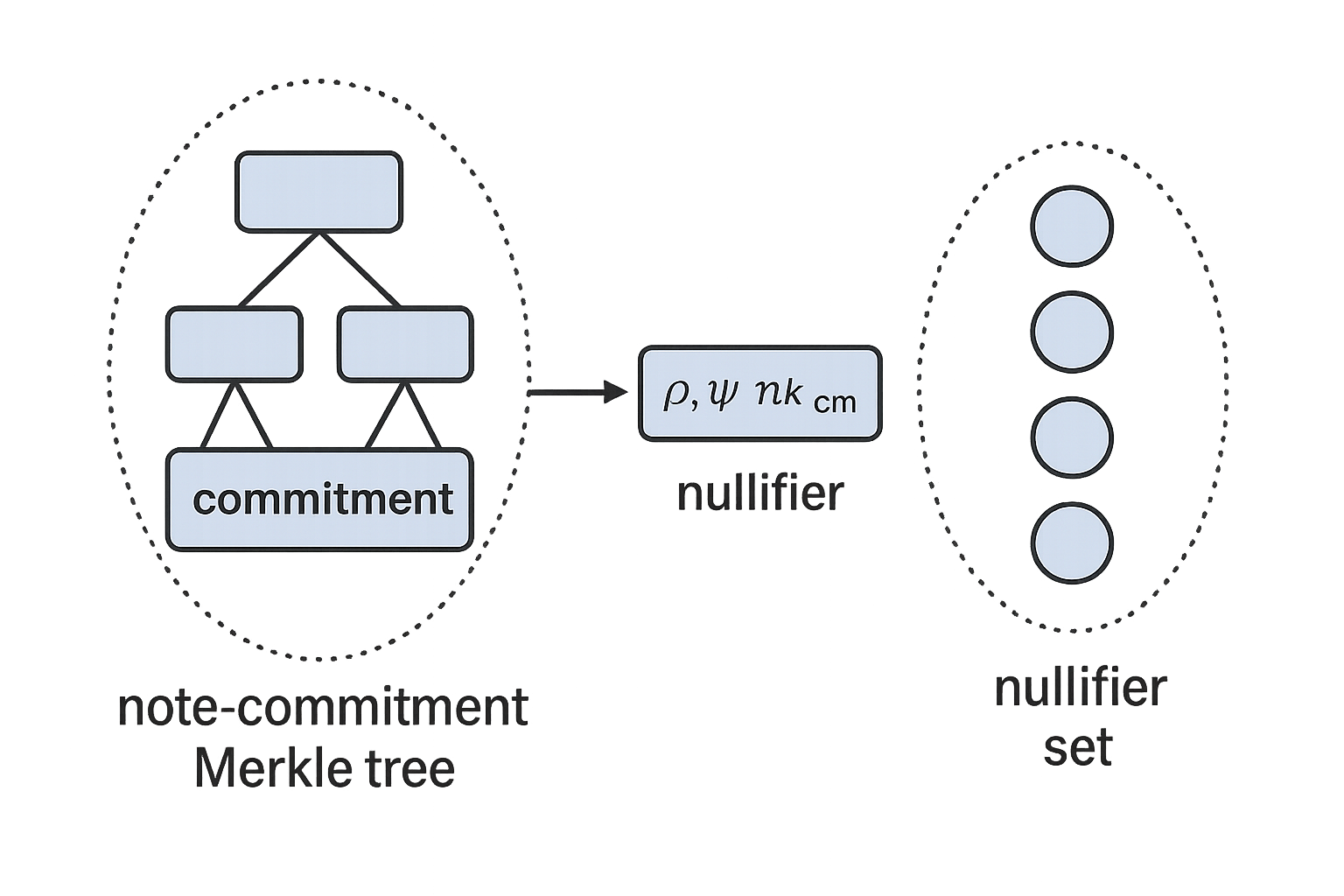
When a new shielded note is created, only its commitment is revealed. This is appended to the global note-commitment Merkle tree, while the note’s actual value and recipient stay private. Because the tree is append-only and doesn’t track spending, a second tag—the nullifier—ensures each note is spent at most once.
A nullifier is a deterministic, unlinkable fingerprint of a note. It’s computed using a pseudorandom function (PRF) keyed by the note’s secret. Only the owner can derive the nullifier, and each note has exactly one2.
“A transaction is not valid if it would have added a nullifier to the nullifier set that already exists in the set.”
The nullifier is publicly revealed and checked against the nullifier set, which is updated each block along with the Merkle tree. This allows the network to reject double-spends while learning nothing about the note itself.
Private membership proof
Zcash uses zk-SNARKs to enforce both constraints—commitment inclusion and nullifier consistency—without revealing which note is spent. Each proof is ~1–2 kB, verifiable in milliseconds, and works even for light clients3.
1. The private link created inside the zk-SNARK
Merkle inclusion:
The prover supplies the note commitment 4 and a Merkle authentication path as private witness data. The circuit enforces:
where is the anchor, a public input representing the Merkle root at block height 5. This confirms that appears somewhere in the historical note-commitment tree.
Nullifier computation:
In the same circuit, the prover recomputes the nullifier using:
where are secrets derived from the note. The output nullifier is made public and bound to the same anchor and commitment.
This internal linkage ensures that the SNARK proves consistency between the revealed nullifier and the private note it was derived from—without revealing anything about the note itself.
2. How the on-chain check works
Each transaction includes the anchor and the nullifier in the public input of the proof. Once the SNARK verifies, every full node checks:
- That the nullifier is not already in the nullifier set .
- If the check passes, the block updates:
This ensures that every nullifier appears at most once—enforcing one-time spendability.
3. Why the two links suffice
- Existence: The Merkle equation certifies that a real commitment already sits in the tree whose root is .
- Uniqueness: The PRF binds a single nullifier to that , and consensus allows each to appear only once.
Hence, any valid transaction must:
- Reference some existing note (via inclusion of ),
- And cannot reuse that note (since its would already be in ).
The inclusion proof and the non-inclusion check are mathematically fixed through the shared variables —inside the SNARK and on-chain.
Limitations of Merkle Trees
Incremental Merkle trees6 are the classic way Zcash records shielded notes7. They have a fixed depth , so the ledger can accept at most commitments before a migration is needed. Every new note becomes a fresh leaf, and the tree’s collision-resistant hashing lets a prover later show inclusion with a -hash path. That path is constant-size and efficient, but the tree’s state grows forever8.
Sharding helps, but doesn’t solve the problem
A natural next step is to shard the Merkle tree. Instead of one monolith, the ledger maintains many sub-trees (e.g., -leaf trees). When a shard fills, a new one is opened, and a small root-of-roots tree tracks the current shard roots. A note’s inclusion path now includes:
- A short intra-shard Merkle path
- One additional hash to reach the root-of-roots
This design keeps proof sizes small and reduces wallet update overhead: clients only need to track changes in shards that contain their notes 9.
But even this is a temporary fix. The root-of-roots is itself incremental and will eventually fill. Historical paths must still be updated as long as the shard is active. State pruning remains difficult because every note ever minted must remain accessible. As a result, ledger size and wallet sync bandwidth grow linearly with protocol lifetime.
Why a set non-inclusion accumulator changes everything
A set non-inclusion accumulator offers a simpler approach to tracking spent notes.
While incremental Merkle trees work perfectly well for inclusion proofs, they cannot efficiently support non-inclusion proofs. The accumulator solves this by folding all notes into a constant-size accumulator value that can handle non-inclusion proofs (and can be easily extended to support inclusion proofs as well). Every insertion is a succinct polynomial-commitment update, and old accumulator states can be discarded—because an IVC (incremental verifiable computation) chain certifies correctness across updates.
The key advantage is simplicity: while Merkle trees require separate handling for commitments and nullifiers, the accumulator provides a single cryptographic primitive that handles non-inclusion proofs. This means we can use the same system for the nullifier set, and extend it to handle note commitments if needed.
The magic lies in the accumulator’s recursive structure: each update witnesses that a vector of notes was inserted without including a particular element . The non-membership claim is upheld step-by-step, proving that each polynomial inserted lacked as a root—meaning was not present. This transforms the problem into one of recursive algebra, not storage.
At the end, proving non-inclusion (“this nullifier was never inserted up to ”) requires only checking that a single polynomial (the one folded into the accumulator) does have as a root.
- The accumulator’s size never grows, no matter how many notes are inserted
- There’s no depth cap or leaf index to exhaust
- Each IVC step is just a few hashes and group ops—efficient even onchain
- You don’t need to track historical state prior to the last epochs—as long as all proofs spanning that range have been generated, the earlier accumulator data can be safely discarded
In short: shielded anonymity can grow indefinitely, with no migrations or tree maintenance. This is the foundation for Project Tachyon’s accumulator design—a simpler system that handles non-inclusion proofs efficiently.
Implementation
The accumulator starts in a trivial state and is updated every time we insert a vector of field elements . After many updates we want to show, for every step in a chosen range , that the inserted vector never contained some element . Instead of storing all past vectors, we fold them into a single curve-point accumulator whose size never grows.
The magic is that while we track more and more nullifiers internally—building a bigger polynomial each time—we only store a single point on-chain. This point acts as a cryptographic summary of all nullifiers we’ve seen, like a Merkle root but without the tree. This means the blockchain state stays tiny, even as we process millions of transactions.
1. Insertion: folding one vector of roots
For the current step we first build its vanishing polynomial
then make a Pedersen commitment to the coefficient vector. One Fiat–Shamir challenge lets us hop to the next state
pub fn insert(roots: &[Fr], a_prev: G1Affine, r: Fr) -> Result<State> {
let poly = poly_from_roots(roots); // a_i(X)
let p_i = commit(&poly.coeffs, r)?; // P_i
let h = hash_points_to_fr(&a_prev, &p_i); // H(A_i,P_i)
let next = a_prev * h + p_i; // A_{i+1}
Ok(State { Accumulator: next.into_affine(), Commitment: p_i })
}Key point: no matter how many vectors we add, Accumulator stays a single point.
2. Proving that a fresh value was not among today’s roots
The verifier will accept only if the polynomial we committed doesn’t vanish at .
-
Evaluate once: . If the proof must abort (v was a root).
-
Shift the commitment so the shifted polynomial does vanish at :
-
Use a second challenge to hop the non-membership accumulator.
pub fn check_non_membership(
roots: &[Fr], v: Fr, r: Fr, s_prev: G1Affine) -> Result<State>
{
let poly = poly_from_roots(roots);
let alpha = evaluate_poly(&poly.coeffs, v); // α = a_i(v)
assert!(!alpha.is_zero()); // must be non-root
let p_i = commit(&poly.coeffs, r)?; // P_i
let p_ip = p_i - POINTS[0] * alpha; // P'_i
let h_p = hash_points_to_fr(&s_prev, &p_ip); // h′ = H(S_i,P′_i)
let next = s_prev * h_p + p_ip; // S_{i+1}
Ok(State { Accumulator: next.into_affine(), Commitment: p_i })
}Because , the shifted commitment now hides a polynomial whose only root at is the one we artificially created—exactly the witness we need for non-membership.
3. Non-membership across a range with IVC
We can create a recursive (IVC) proof with base case is and repeat the above step for every to make a ranged claim.
- In the circuit we start from snapshot .
- At each iteration we witness and apply the
check_non_membershiphop. - The accumulator moves from to .
- Only the current state crosses the IVC boundary; earlier data are discarded.
After hops the verifier sees .
If S_m opens to zero at , then—by induction—every intermediate polynomial was proven to evaluate non-zero at . Hence never appeared in any root vector .
4. Why this matters for Zcash-style nullifier checks
- O(1) state:
Accumulatoris one point no Merkle depth cap. - Forget history: once the IVC proof exists, we can delete every old vector.
- Cheap per block: each hop is a couple of hashes and group operations
- Scalable non-membership: perfect for showing a nullifier never appeared, without keeping the nullifier set on-chain.
In practice, replacing Zcash’s append-only Merkle trees with this accumulator would remove anchor leakage and tree maintenance, while still proving that a nullifier is unique.
Conclusion
A vector-commitment accumulator gives Zcash a simpler approach to tracking spent notes: constant-size state that efficiently handles non-inclusion proofs (and can be extended to support inclusion proofs). This eliminates depth caps and tree migrations, while still providing the same security properties as Merkle trees.
Real-world deployment still has open questions—metadata privacy, lightweight witness updates, etc. Check out my implementations of this accumulator below.
| Prototype | Idea | Code |
|---|---|---|
| PCS-only | accumulator + polynomial commitment | https://github.com/0xWOLAND/set-noninclusion |
| Folded proofs | same accumulator, block-by-block recursion with the zkVM SP1 | https://github.com/0xWOLAND/sp1-noninclusion built with SP1 |
For the full design sketch, see Sean Bowe’s HackMD.
Appendix
The vector-commitment accumulator guarantees existence (the value really was inserted) and uniqueness (no two different vectors can open to the same commitment at the same index) for two independent reasons:
Existence in the IVC non-membership chain
For non-inclusion, each IVC step asserts . Because the polynomial encodes exactly the vector inserted at step , the statement ” was not in ” is true iff the evaluation is non-zero. The final recursive proof therefore certifies that for every step in the range, was not a coordinate of any inserted vector. That is an existential statement about the entire history, achieved with only verifier work.
Uniqueness of a nullifier-style opening
If we swap the vector commitment for one that derives a nullifier‐like output (e.g. include the index and value in a PRF), the uniqueness follows the same logic: the PRF output is a function of a single valid opening, and the binding of the commitment ensures no second, distinct opening can produce the same output without violating discrete-log or collision-resistance.
In short, the algebraic binding of the commitment bases anchors existence, while their linear independence enforces uniqueness—properties that survive each IVC update and give the accumulator the same double-spend resistance Merkle nullifiers provide, but with constant-size state and proofs.
Footnotes
-
A note is a cryptographic representation of a value that can be spent by the holder of the corresponding shielded spending key ↩
-
In Orchard, the nullifier is computed as a PRF fo the note’s two randomizers , the owner’s nullifier-deriving key , and the commitment . ↩
-
A light client verifies state transitions using succinct proofs instead of downloading the full chain. This allows secure operation on low-resource devices. ↩
-
Because is a binding Sinsemilla commitment, two different openings and cannot map to the same curve point without either (i) finding a collision in the hash-to-curve function or (ii) solving a discrete-log problem—both assumed infeasible. If you tweak any field of the note or choose a new blinding scalar , you inevitably get a different point and hence a different . Since the Merkle‐path inside the zk-SNARK ties the spend to the exact that already sits in the tree, you can’t “swap in” an alternative commitment; you would first have to mint that new in a separate transaction. And because the nullifier is a PRF that explicitly includes , changing the commitment would also change the nullifier, so the on-chain double-spend check still holds. ↩
-
Each block in Zcash has a note-commitment tree of height. The genesis block is height 0, and each subsequent block increments this height by 1. ↩
-
An incremental Merkle tree is a binary tree that supports efficient, append-only updates: each new element is added as the next available leaf, and only the hashes along its path to the root are recomputed. This allows the Merkle root to evolve over time without rebuilding the whole tree, enabling short inclusion proofs that stay constant in size. ↩
-
Zcash uses incremental Merkle trees to maintain a commitment tree of all shielded notes. As each note is created, its commitment is appended to the next empty leaf. Internal nodes are updated on-the-fly, and the Merkle root evolves incrementally. Inclusion proofs are short (one hash per level), and the current root is used as a public anchor in each transaction. This enables privacy-preserving spending proofs without revealing which note is spent. ↩
-
While the tree state grows, wallet witness updates can be made efficient: a trusted third party can provide just advice that lets clients update their witnesses through insertions without downloading every new leaf. This is exactly how Zashi currently handles witness updates by having a server provide compact update hints that let wallets stay in sync with minimal bandwidth. ↩
-
Sharding solves UX problems around note detection and spendability. See this forum post for details on the tradeoffs and design. ↩